Teaching the Angle Sum Theorem in Triangles

Missing angles in a triangle leads us to the angle sum theorem which states that there are 180˚ in every triangle. Really??? In EVERY triangle? How is this possible?? There are a lot of theorems in geometry that we TRY to prove to students, but perhaps it's difficult for everyone to make the connection. The angle sum theorem in triangles though is a theorem that has a low floor and should allow more students to really internalize the idea.

Here are a few ideas for "proving" to students that there are 180˚ in the interior angles of EVERY triangle.

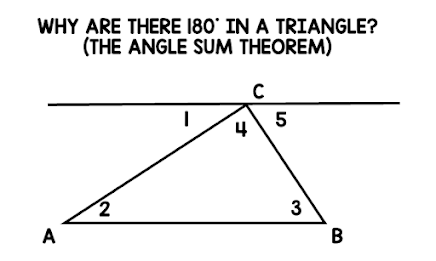
1) Use an actual proof:

The proof I use requires students to know some information about parallel lines. Let me explain...

Give students the information that the two lines that look parallel are parallel, then use the following simple proof.

2) Use Geogebra:

Although using geogebra often isn't a rigorous proof, I get oohs and aaahhhs when I use this idea. You can google Geogebra sum of angles in a triangle to get lots of different premade sketches that you can use with your class. Depending on their level and the tech you have available, you may want to choose different possibilities. Here's one example:

3) Drawing a Model on Paper

Have students draw a medium/large triangle - it can be any kind of triangle. Outline the edges of the triangle. (This will be important in a minute!) Cut the triangle out.

Cut off the angles of the triangle. Because you outlined the edges of the triangle, you can tell which angles of these cut out pieces are the angles of the triangle.

Put the angles back together to show that they form a line.

Don't want to have your class do it live? Show a video instead. Try this one: Video to show 180˚ in a triangle. [ There are many videos available - I just googled video to show that there are 180˚ in a triangle.]

Overall, the key to successful teaching of the Triangle Angle Sum Theorem is to provide students with a variety of problems and exercises that allow them to practice the theorem in different contexts. In addition, using visual aids, hands on activities, and proofs will help them understand the underlying concepts.

Need something for your students to use to practice? I have you covered! You can use this coloring activity, pile on activity, and maze. Check it out below!